The following is an aerodynamic shape optimization case for the NACA0012 airfoil in subsonic conditions.
Case: Airfoil aerodynamic optimization Geometry: NACA0012 Objective function: Drag coefficient (CD) Lift coefficient (CL): 0.5 Design variables: 20 free-form deformation (FFD) points moving in the y direction, one angle of attack Constraints: Symmetry, volume, thickness, and lift constraints (total number: 34) Mach number: 0.294 (100 m/s) Reynolds number: 6.667 million Mesh cells: ~4,500 Solver: DARhoSimpleFoam

Fig. 1. Mesh and FFD points for the NACA0012 airfoil
The “runScript.py” is similar to the one used in the NACA0012 low speed case with the following exceptions:
-
In the global parameters, we provide additional variable such as “T0” (far field temperature) and “rho0” (a reference density to normalize CD and CL). In addition, we provide the absolute value of pressure “p”, instead of the relative value use in the low speed case.
-
In “primalBC”, we need to set boundary condition for temperature “T0”.
-
We use “DARhoSimpleFoam”, which is an OpenFOAM built-in compressible flow solver suitable for subsonic conditions. Accordingly, we set “flowCondition” to “Compressible”.
-
To ensure a robust convergence, we need to bound the variables when solving the primal. This is done by setting lower and upper bounds in “primalVarBounds” for all variables.
To run this case, first download tutorials and untar it. Then go to tutorials-main/NACA0012_Airfoil/subsonic and run the “preProcessing.sh” script to generate the mesh:
./preProcessing.sh
Then, use the following command to run the optimization with 4 CPU cores:
mpirun -np 4 python runScript.py 2>&1 | tee logOpt.txt
The case ran for 50 steps and took about 25 minutes using Intel 3.0 GHz CPU with 4 cores. According to “logOpt.txt” and “opt_SLSQP.txt”, the initial drag is 0.015226161 and the optimized drag is 0.013617362 with a drag reduction of 10.6%.
The evolution of pressure and shape during the optimization is as follows.
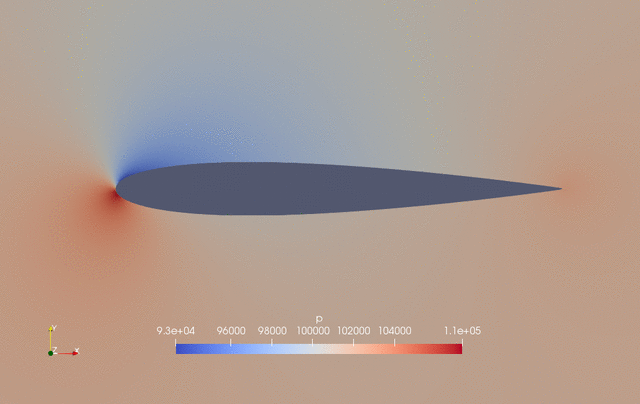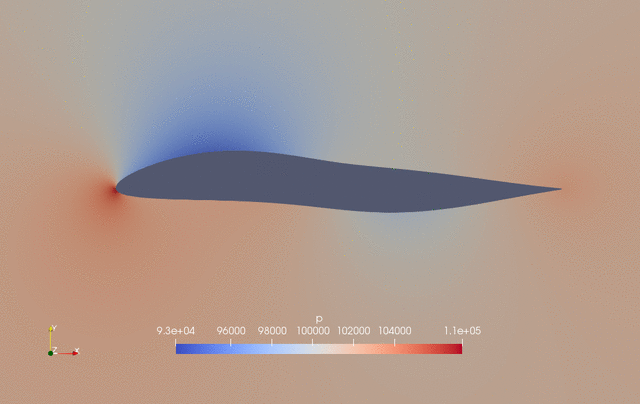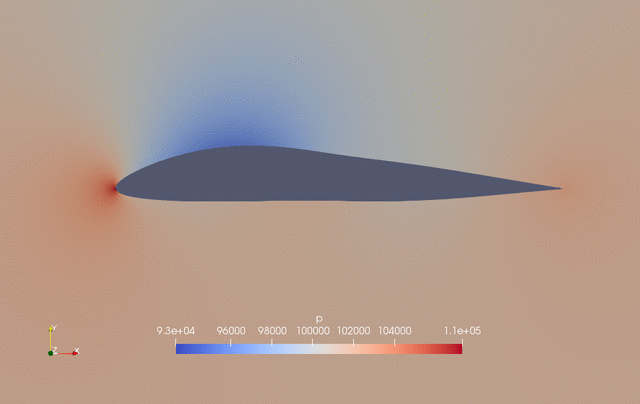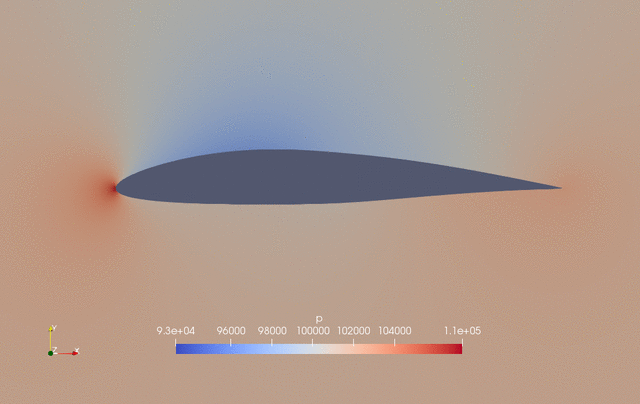
Fig. 2. Pressure and shape evolution during the optimization process