The following is an aerodynamic optimization case for the MD 30N30P multi-element Airfoil
Case: Multi-element Airfoil
Geometry: MD 30N30P
Objective function: Lift coefficient
Design variables:
20 FFD points for the main element shape
Pitch variables for the slat and flap
Translation variables for the slat and flap
Angle of attack
27 in total
Constraints: Drag coefficient
Mach number: 0.2
Reynolds number: 4.5 million
Mesh cells: ~13,569
Solver: DARhoSimpleFoam
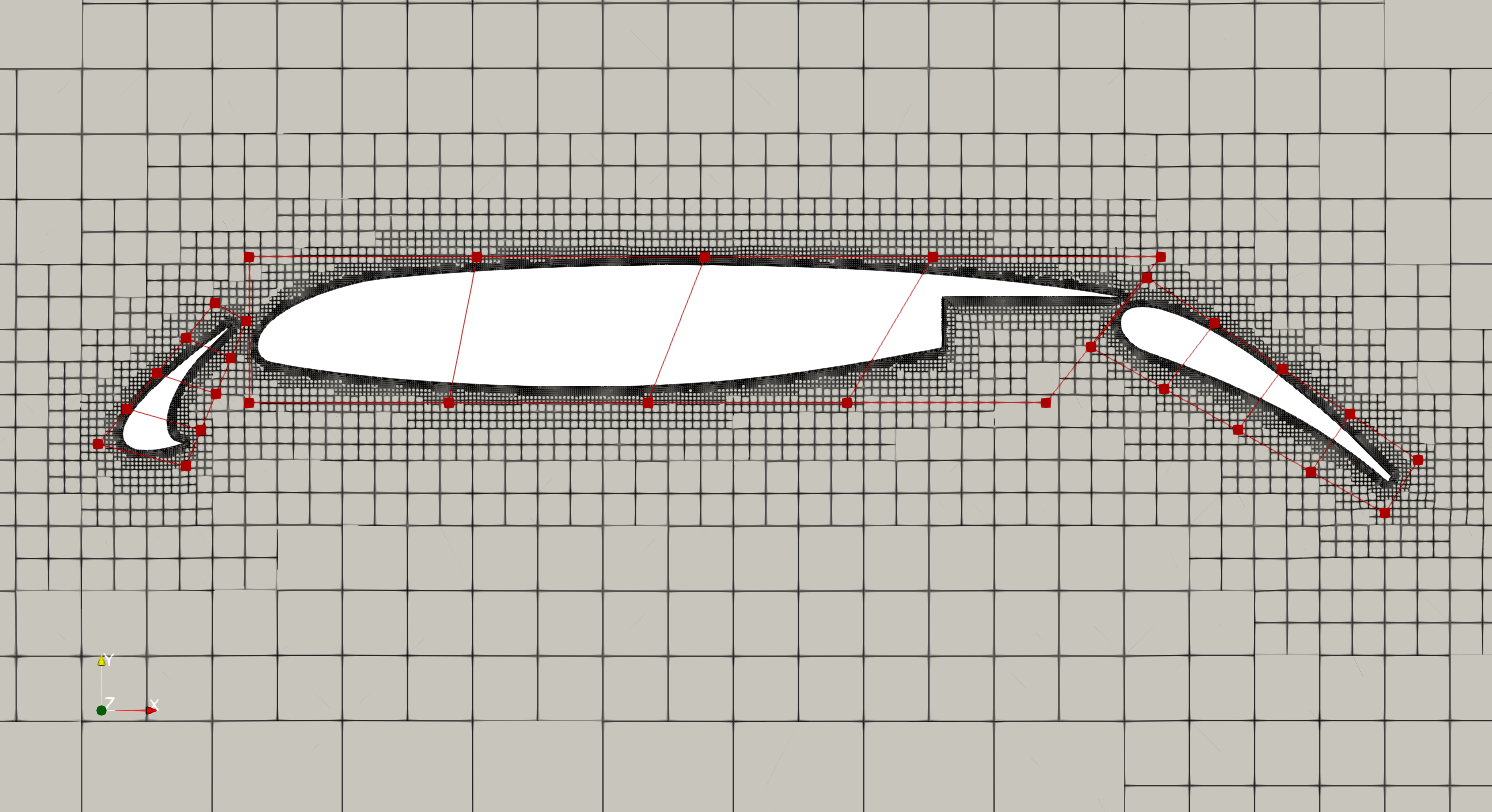
Fig. 1. Mesh and FFD points for the 30N30P multi-element airfoil
In this tutorial, we set up three FFD blocks (see Fig.1) that cover the slat (vol=0), main airfoil (vol=1), and flap (vol=2). Check the genFFD.py file in the FFD folder. We use the snappyHexMesh utility in OpenFOAM to generate the mesh.
In terms of the design variables setup, we use 20 FFD points to change the shape of the main airfoil element. Then, we use the following functions to rotate and translate the slat and flap:
def twistslat(val, geo):
for i in range(2):
geo.rot_z["slatAxis"].coef[i] = -val[0]
def translateslat(val, geo):
C = geo.extractCoef("slatAxis")
dx = val[0]
dy = val[1]
for i in range(len(C)):
C[i, 0] = C[i, 0] + dx
for i in range(len(C)):
C[i, 1] = C[i, 1] + dy
geo.restoreCoef(C, "slatAxis")
def twistflap(val, geo):
for i in range(2):
geo.rot_z["flapAxis"].coef[i] = -val[0]
def translateflap(val, geo):
C = geo.extractCoef("flapAxis")
dx = val[0]
dy = val[1]
for i in range(len(C)):
C[i, 0] = C[i, 0] + dx
for i in range(len(C)):
C[i, 1] = C[i, 1] + dy
geo.restoreCoef(C, "flapAxis")
The rotation and translation are achieved by rotating the reference axis, e.g., geo.rot_z[“slatAxis”].coef[i], or translating the coordinates of the reference axis, e.g., C[i, 0] = C[i, 0] + dx.
To use the above functions, we need to first define the reference axis for slat and flap. The reference axis for the slat is defined near its trailing edge while the reference axis for the flap is define near its leading edge.
# Slat refAxis
xSlat = [-0.027, -0.027]
ySlat = [-0.109, -0.109]
zSlat = [0.0, 0.1]
cSlat = pySpline.Curve(x=xSlat, y=ySlat, z=zSlat, k=2)
DVGeo.addRefAxis("slatAxis", curve=cSlat, axis="z", volumes=[0])
# Flap refAxis
xFlap = [0.875, 0.875]
yFlap = [0.014, 0.014]
zFlap = [0.0, 0.1]
cFlap = pySpline.Curve(x=xFlap, y=yFlap, z=zFlap, k=2)
DVGeo.addRefAxis("flapAxis", curve=cFlap, axis="z", volumes=[2])
For the objective function, we want to maximize the lift while keeping the drag constant.
# Add objective
optProb.addObj("CD", scale=1)
# Add physical constraints
optProb.addCon("CL", lower=CL_target, upper=CL_target, scale=1)
To run this case, first download tutorials and untar it. Then go to tutorials-main/30N30P_MultiElement_Airfoil and run the “preProcessing.sh” script to generate the mesh:
./preProcessing.sh
NOTE: the above command will just download the mesh. If you want to re-generate the mesh or change the mesh density, run preProcessing_reGenMesh.sh instead (the mesh generation process make take up to an hour). Then, use the following command to run the optimization with 4 CPU cores:
mpirun -np 4 python runScript.py 2>&1 | tee logOpt.txt
The case ran for 43 iterations. The initial lift coefficient is 3.416 and the optimized lift coefficient is 3.509 with an increase of 2.7%.
NOTE: By default, this case uses the Jacobian free option in daOptions: “adjJacobianOption”: “JacobianFree”. This means that you need to compile the AD version of OpenFOAM and DAFoam (see here). If you use the Docker image, they have been compiled so no additional action is needed. If you haven’t compiled the AD version, set this: “adjJacobianOption”: “JacobianFD”.

Fig. 2. Evolution of airfoil shape and velocity distribution