The following tutorial is an optimization of the NACA0012 airfoil to reduce drag while maintaining a predefined lift value. This shape optimization is handled via a surrogate based optimization method utilizing the SMT python package.
Case: Airfoil aerodynamic optimization Geometry: NACA0012 Objective function: Drag coefficient (CD) Lift coefficient (CL): 0.5 Design variables: 8 free-form deformation (FFD) points moving in the y direction, one angle of attack Constraints: Symmetry, volume, thickness, and lift constraints Mach number: 0.02941 (10 m/s) Reynolds number: 0.6667 million Mesh cells: ~4,000 Solver: DASimpleFoam

Fig. 1. Mesh and FFD points for the NACA0012 airfoil
The surrogate based optimization capability in DAFoam is designed in such a way that any DAFoam opitmization case can be converted to a surrogate based optimization case by adding one additional python file to configure the surrogate optimization. For this variation of the NACA0012, this file is runScript_SBO.py which can be found in the tutorials under the NACA0012_Airfoil/incompressible case folder.
The first part of runScript_SBO.py is to import the necessary packages and the case setup (the OpenMDAO model):
import numpy as np # use numpy for arrays
from runScript import prob as NACA0012 # import OpenMDAO model of airfoil from runScript
from dafoam.pyDAFoam import surrogateOptimization # import surrogate optimization class
Numpy arrays are required by SMT for the design variable arrays. The secong import, from runScript import prob as NACA0012 imports the OpenMDAO model from runScript.py and renamed to NACA0012. This model will be passed to the surrogate optimization class to perform the actual optimization. The last import, from dafoam.pyDAFoam import surrogateOptimization, imports the surrogate optimization class which will execute the optimization.
Following this, we need to define the design variables of the problem:
# define design variables (name & size)
dvNames = ["shape", "patchV"]
dvSizes = [8, 2]
# prescribe bounds on design variables
xlimits = np.array([[0.0, 0.05]] * 10)
# adjust bounds for AOA, fix velocity to 10m/s
xlimits[-1] = [1, 1.5]
xlimits[-2] = [10, 10 + 1e-9]
dvNames lists only the names of the design variables which must match the naming convention in runScript.py. dvSizes gives the number of actual design variables (e.g. The shape design variable uses 8 FFD points, hence the first element of dvSizes is 8. patchV is an array which contains the far field velocity and angle of attack, hence the size is given as 2). In total, this gives 10 points for which we must prescribe design variable bounds.
To prescribe bounds, we first define xlimits = np.array([[0.0, 0.05]] * 10), where the design variables are organized by the first 8 entries corresponding to the FFD point displacements and the final two entries are for the far field velocity and angle of attack, respectively.
This initial setup uses a lower bound of 0.0 to an upper bound of 0.05 for all 10 design variables. These bounds will work for the FFD points, but must be adjusted for the far field velocity and angle of attack. The far field velocity is a fixed value, however, SMT does not support design variables with equal upper and lower bounds. The easiest solution is to give an upper and lower bound which differ by only a small amount. This is done for the far field velocity by setting xlimits[-2] = [10, 10 + 1e-9]. Lastly, the angle of attack needs a different set of bounds which is set as xlimits[-1] = [1, 1.5].
With the design variables and the design variable bounds being properly defined, we next define the objective function and constraint functions. For this optimization case, the objective function is to minimize drag ($C_{d}$) subject to the following constraints:
-
$C_{l}$ = 0.5
-
0.5 $\leq$ airfoil thickness $\leq$ 3
-
1 $\leq$ airfoil volume
-
0.8 $\leq$ LE radius
To implement this into the surrogate based optimization, the user defines:
objFunc = 'scenario1.aero_post.CD'
cons = ['scenario1.aero_post.CL', 'geometry.thickcon', 'geometry.volcon', 'geometry.rcon']
conWeights = [1e10, 10, 10, 1e2]
consEqs = ["x - 0.5", "0.5 <= x <= 3", "1 <= x", "0.8 <= x"]
The names used for the objective function (objFunc) and constraint function(s) (cons) must match the naming convention used in runScript.py. conWeights is an array containing the weight(s) for the constraint function(s). A higher weight will strongly enforce the constraint, a lower weight will relax the constraint. The user should prescribe the weights according to how strict the constraint should be.
The surrogate based optimization can handle multiple constraint functions which are defined in consEqs. It is given as a string and must always use x for the variable. There are two types of constraints supported: equality constraints and inequality constraints. Inequality constraints should be typed out without modification. Equality constraints need to be rewritten as a function of x. For example, since we want to enforce that $C_{l} = 0.5$, we can rewrite this as $C_{l} - 0.5 = 0$ then replace $C_{l}$ with $x$ to get the constraint equation of $x - 0.5 = 0$.
The last step before running the optimization is to define the surrogateOptions dictionary and pass the dictionary to the surrogateOptimization class:
surrogateOptions = {
"criterion" : "EI", # criterion for next evaluation point
"iters" : 10, # num iterations to optimize function
"numDOE" : 15, # number of sampling points
"seed" : 43, # seed value to reproduce results
"dvNames" : dvNames, # names of design variables
"dvSizes" : dvSizes, # number of points for each design variable
"dvBounds" : xlimits, # design variable bounds
"objFunc" : objFunc, # objective function
"cons" : cons, # quantities to constrain
"conWeights" : conWeights, # constraint weights
"consEqs" : consEqs, # constraint equations
"surrogate" : "MGP", # which surrogate model to use (Kriging-based)
}
surrogateOptimization(surrogateOptions, NACA0012) # pass surrogateOptions and OpenMDAO model to surrogateOptimization class
The surrogateOptions dictionary defines various parameters for the optimization problem. We use the Expected Improvement scheme (EI) as our evaluation criterion. The number of iterations (iters) is set to 10. These are the iterations used to optimize the objective function. For this surrogate optimization we must also decide how many Design of Experiment (numDOE) points to use. A higher number will increase accuracy but will also increase run time. Too few points, however, and the optimization will struggle to find the correct optimal point. It should be noted that the numDOE points are generated using a random number generator (RNG). To be able to reproduce results, a seed value is given. The next 7 entries relate to the design variable definitions, objective function, and constraint definitions which were covered earlier in this section. Here we simply pass these values into the surrogateOptions dictionary. Lastly, we prescribe a specific surrogate model to use, MGP. The default is KRG, but different models produce different results. The MGP model works well in producing a good optimal point, hence its selection. Detailed information on each model can be found here
To run this case, first download the tutorials and untar it. Then go to NACA0012_Airfoil/incompressible and run the preProcessing.sh script to generate the mesh. Once that completes, run the optimization using the following command:
mpirun -np 4 python runScript_SBO.py 2>&1 | tee logOpt.txt
The optimization reduced drag by 17.12% with $C_{l} = 0.502$
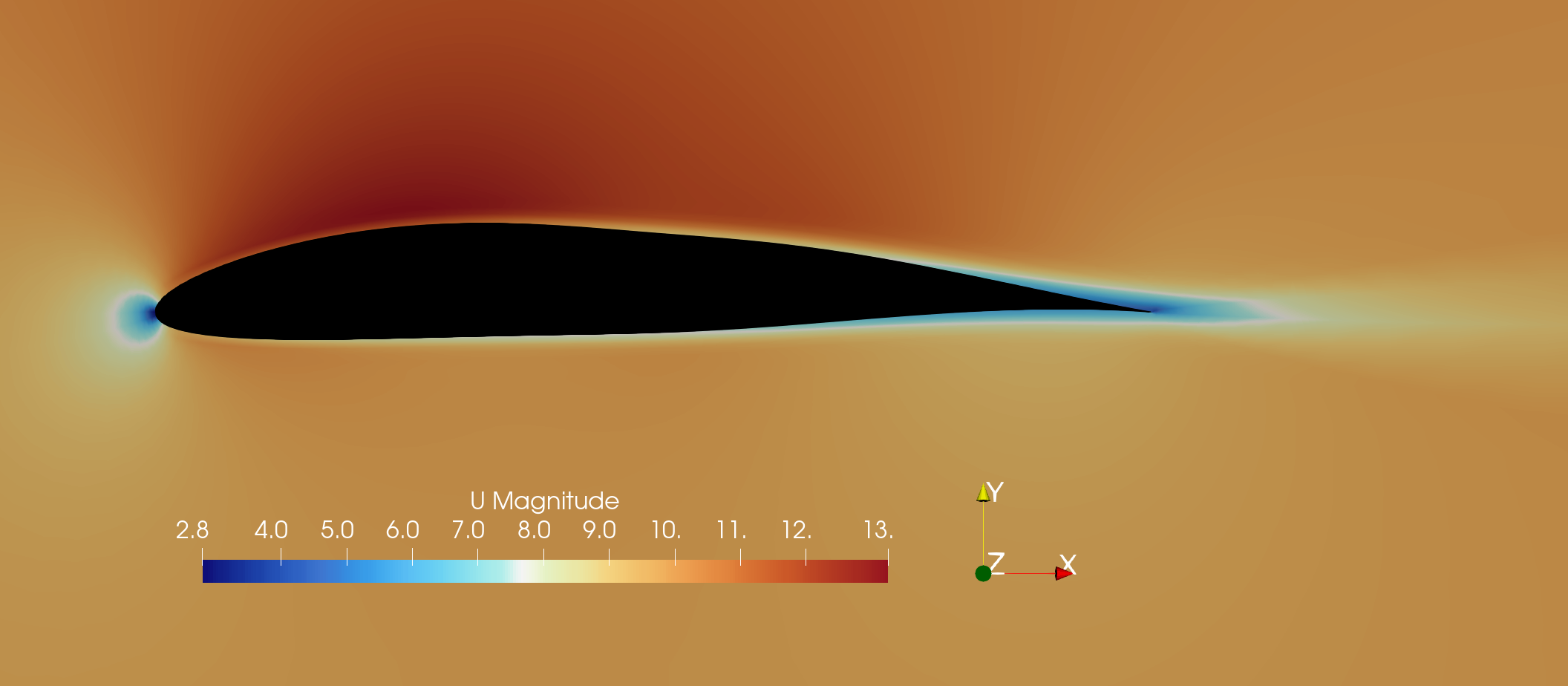
Fig. 2. Optimized NACA0012 airfoil velocity field